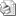
(дадатны кірунак пазначана + j)

). Гэты ж вектар можа быць зададзены і ў палярнай сістэме каардынат. Гэта значыць праз даўжыню вектара I і кут павароту ψ (пазначым яе rθ). Палярнай сістэме каардынат адпавядае паказальная форма запісу комплекснага ліку

I = Ie^jψ,

О

Асноўныя аперацыі з комплекснымі лікамі

Складанне

Хай два комплексных ліку зададзены ў алгебраічнай форме запісу

z1 = a1 + j · b1; z2 = a2 + j · b2

трэба знайсці суму гэтых лікаў

z3 = z1 + z2 = (a1 + j · b1) + ( a2 + j · b2) = (a1 + a2) + j · (b1 + b2) = a3 + j · b3.

Гэта значыць пры складанні сапраўдныя часткі складаюцца з сапраўднымі, а ўяўныя з ўяўным.

z₃ = z₁ - z₂ = (a₁ + j·b₁) - (a₂ + j·b₂) = (a₁ - a₂) + j·(b₁ - b₂) = a₃ + j·b₃.

Множанне

Хай два комплексных ліку зададзены ў паказальнай форме запісу

z₁ = z₁ e ^jφ₁ ;  z₂ = z₂ e ^jφ₂

z₃ = z₁·z₂ = z₁ e ^jφ1· z₂ e ^jφ2 = z₁· z₂ e ^j(φ1+φ2)

Тое значыць пры памнажэньні модулі перамнажаюцца, а аргументы складаюцца

Дзяденне

z₁ = z₁ e ^jφ₁ ;  z₂ = z₂ e ^jφ₂

z₃ = z_1: z₂ = z₁ e ^jφ₁ : z₂ e ^jφ₂ = (z_1/ z₂ ) e ^{j(φ₁ - φ₂)}

Аперацыi з камплекснымi лiкамi на iнжынерных калькулятарах

Першае, на что трэба звярнуць увагу при включеннi калькулятара гэта тое, у якiх адзiнках вымяраются вуглы.

Магчымыя варыянты DEG, RAD, GRAD

Звычайна ў разліках выкарыстоўваюць градусы, таму на дысплеі калькулятара павінна гарэць DEG ( або D). На калькулятары над кнопкамі маюць «другую функцыю» (па-англійскі second functions, скарочана 2ndf)

П Р Ы К Л А Д 1

П Р Ы К Д А Д 2

П Р Ы К Л А Д 3

П Р Ы К Л А Д 4

П Р Ы К Л А Д 5