КОМПЛЕКСНЫЕ ЧИСЛА 
 Комплексное число – упорядоченная пара чисел 
I = a + j·b,
 где a, b – вещественные числа; j – мнимая единица (в математике обозначают i). По определению j = √-1

Форма записи комплексного числа a + jb называется алгебраической, где a называется действительной частью комплексного числа; b – мнимой частью комплексного числа. Чтобы не путать комплексные числа с действительными числами комплексные числа подчёркиваются, например U .

Геометрическая интерпретация комплексного числа – точка (или вектор) на плоскости.

По оси абсцисс расположена ось действительных чисел (положительное направление обозна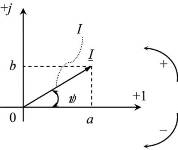чено +1), а по оси ординат – ось мнимых чисел (положительное направление обозначено +j).

Проекция вектора на ось +1 – действительная часть, а проекция на ось +j – мнимая часть. Таким образом, алгебраическая форма записи соответствует декартовой (прямоугольной) системе координат (обозначим её xy).

Этот же вектор может быть задан и в полярной системе координат. То есть через длину вектора I и угол поворота ψ (обозначим её rθ). Полярной системе координат соответствует показательная форма записи комплексного числа 

I = Ie^jψ,

 где I – модуль комплексного числа; ψ – аргумент (или попросту угол)

Обе формы записи (алгебраическая и показательная) используются при расчётах: складывать и вычитать комплексные числа удобно в алгебраической форме записи, а делить и умножать – в показательной. Следовательно, нужно уметь переводить комплексные числа из алгебраической формы записи в показательную (→rθ) и из показательной в алгебраическую (→xy).

Пусть комплексное число задано в алгебраической форме I = a + jb, а требуется найти модуль I и угол ψ. По теореме Пифагора определяем модуль I = √а² +b² а угол 
ψ = arctan (b/a)
 (если a < 0, то к результату надо прибавить (отнять) 180°).

Обратный переход из показательной формы в алгебраическую производят по
формуле Эйлера. Пусть комплексное число задано в показательной форме
I = Ie^jψ, а требуется найти действительную a и мнимую b части. Из того же рисунка видно, что прилежащий катет a это произведение гипотенузы I на косинус угла ψ , а противолежащий катет b это произведение гипотенузы I на синус угла ψ. Таким образом  I =Ie^jψ = I cos ψ + j I sin ψ.

Основные операции с комплексными числами

Сложение

Пусть два комплексных числа заданы в алгебраической форме записи

z₁ = a₁ + j·b₁; z₂ = a₂ + j·b₂ нужно найти сумму этих чисел

z₃= z₁ + z₂ = (a₁ + j·b₁) + (a₂ + j·b₂₎ = (a₁ + a₂) + j·(b₁ + b₂) = a₃ + j·b_3.

То есть при сложении действительные части складываются с действительными, а мнимые с мнимыми.

Вычитание – аналогично:

z₃ = z₁ - z₂ = (a₁ + j·b₁) - (a₂ + j·b₂) = (a₁ - a₂) + j·(b₁ - b₂) = a₃ + j·b₃.

Умножение

Пусть два комплексных числа заданы в показательной форме записи

z₁ = z₁ e ^jφ₁ ;  z₂ = z₂ e ^jφ₂ нужно найти произведение этих чисел

z₃ = z₁·z₂ = z₁ e ^jφ1· z₂ e ^jφ2 = z₁· z₂ e ^j(φ1+φ2)

То есть при умножении модули перемножаются, а аргументы складываются

Деление

Пусть два комплексных числа заданы в показательной форме записи

z₁ = z₁ e ^jφ₁ ;  z₂ = z₂ e ^jφ₂ нужно найти частное этих чисел

z₃ = z_1: z₂ = z₁ e ^jφ₁ : z₂ e ^jφ₂ = (z_1/ z₂ ) e ^{j(φ₁ - φ₂)}

То есть при делении модули делятся, а аргументы вычитаются.

Операции с комплексными числами на инженерных калькуляторах

Первое на что нужно обратить внимание при включении калькулятора это, в каких единицах измеряются углы.

Возможные варианты DEG, RAD, GRAD

Обычно в расчётах используют градусы, поэтому на дисплее калькулятора должно гореть DEG (или D).

На калькуляторе над кнопками располагают «вторую функцию» (англ. second functions сокращённо 2ndf)

П Р И М Е Р  1

П Р И М Е Р  2

П Р И М Е Р 3

П Р И М Е Р  4

П Р И М Е Р 5

П Р И М Е Р 6